Conjecture de Goldbach :
Tout nombre entier pair supérieur à 3
peut s’écrire comme la somme de deux nombres premiers.
D'aspect trivial, cette conjecture a tenu pendant 271 ans !
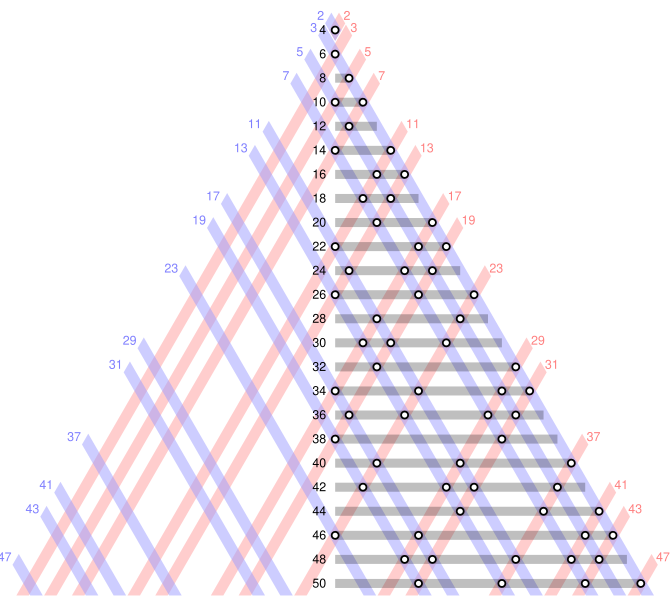 |
| Illustration graphique de la conjecture de Goldbach sur les nombres pairs de 2 à 50 (Wikimedia) |
La majorité des mathématiciens pense que la conjecture de Goldbach est vraie, surtout sur des considérations statistiques axées sur la répartition probabiliste des nombres premiers :
plus le nombre est grand, plus il y a de manières disponibles pour le
représenter sous forme de somme de deux ou trois autres nombres, et la
plus « compatible » devient celle pour qui au moins une de ces
représentations est constituée entièrement de nombres premiers.
Harald Helfgott a démontré la version faible de la conjecture de
Goldbach, à savoir que "tout nombre impair plus grand que 5 est la somme
de trois nombres premiers". C'est différent de la version dite forte
qui correspond à cet autre énoncé : "Tout nombre pair plus grand que 4
est la somme de deux nombres premiers". La conjecture forte reste encore
un mystère à élucider.
Harald Helfgott, docteur en mathématiques de l'université de Princeton et est chargé de recherche (CR1) au CNRS/École normale supérieure, à Paris.
Vous pouvez toujours essayer de la comprendre en la lisant ici :
La conjecture de Goldbach dans la culture :
- En 2007, Luis Piedrahita et Rodrigo Sopeña produisent le film espagnol La Cellule de Fermat (es) (La Habitación de Fermat) mettant en scène un jeune mathématicien qui affirme faussement avoir démontré la conjecture et un vieux mathématicien qui, lui, l’aurait démontrée.
- Le roman Oncle Petros et la conjecture de Goldbach [détail des éditions], d’Apostolos Doxiadis, raconte l’histoire fictive d’un mathématicien ayant consacré sa vie professionnelle à la seule conjecture de Goldbach, gaspillant ainsi ses ressources intellectuelles et se mettant lui-même à l’écart de la vie scientifique et de sa famille. Le roman en profite surtout pour fournir un éclairage culturel sur quelques mathématiciens et logiciens du début du siècle (Kurt Gödel, Alan Turing, Srinivasa Ramanujan, Godfrey Harold Hardy …) et les rapports entre leurs différents travaux. Afin de faire de la publicité pour le livre Uncle Petros and Goldbach’s Conjecture de Apostolos Doxiadis, l’éditeur britannique Tony Faber offrit en 2000 un prix de 1 000 000 $ pour une preuve de la conjecture. Le prix ne pouvait être attribué qu’à condition que la preuve soit soumise à publication avant avril 2002. Il n’a jamais été réclamé.
- Le roman Le Théorème du Perroquet, de Denis Guedj, met en scène un mathématicien qui, au fond de l’Amazonie, réussit à démontrer la conjecture de Goldbach. Refusant de la livrer à l’humanité, il se suicide en brûlant ses recherches. Mais avant, il la fait apprendre par son perroquet. Des mafieux veulent s’approprier l’oiseau mais ce dernier reste muet. Excédés, ils l’abattent. Le roman se termine dans la forêt où le perroquet, blessé, récite la démonstration aux autres animaux. Elle demeure ainsi inconnue des hommes.
Sources : Wikipedia




10 commentaires:
Oula ! Je n'ai pas osé tout lire, je préfère regarder les images de tartes géométriques ! ;-)
Et tu as bien raison :-q
Harald Helfgott a démontré la version faible de la conjecture de Goldbach, à savoir que "tout nombre impair plus grand que 5 est la somme de trois nombres premiers". C'est différent de la version dite forte qui correspond à cet autre énoncé : "Tout nombre pair plus grand que 4 est la somme de deux nombres premiers". La conjecture forte reste encore un mystère à élucider.
Cordialement
Greg
Merci Greg pour cette précision, je viens de modifier mon post en ce sens.
Quel est le resultat avec 68 S'il vous plait :'(
D'après ma formule, il y a au moins 2 possibilités de somme , car pour tout nombre pair supérieur ou égal à 64,il y a au moins 2 possibilités.
En réalité, il a 3 possibilités qui sont 1 + 67, 7 + 61, 31 + 37.
Vous me direz que le nombre 1 n'est pas premier; mais en 1742 il l'était.
Et je signe
JP MORVAN
Si tous nombres impaire peuvent s'écrire comme la somme de 3 nombres premiers, ça implique forcément que tous les nombres paires peuvent s'écrire comme la somme de 2 nombres premiers. Donc la conjecture de Goldbach est démontrer Non ?
Madame,
je ne pense pas qu'il existe de portrait du mathématicien Christian Goldbach. On trouve cependant partout sur internet, et en particulier sur votre excellent site, une image censée être son portrait. Il est pourtant évident qu'il s'agit d'une photographie, et qu'elle représente un homme du XIXè siècle, compte-tenu de son habillement. Il est donc certain qu'il ne peut s'agir de Christian Golbach, auteur de la conjecture, mort en 1764 ! Si internet est un prodigieux vecteur d'informations, c'est aussi (hélas) un efficace multiplicateur d'erreurs et d'informations incontrolées. Celle-ci pourrait être corrigée.
Cordailement
Philippe Gautrot
Je précise mon précédent post : ce n'est pas un portrait de Christian Goldbach mais une photographie d'Hermann Grassmann. Cette erreur d'attribution traine un peu partout sur internet, malgré l'évidence. Cordialement. Ph. Gautrot
Merci Philippe pour votre vigilance ! L'image est retirée de l'article.
Ce type de confusion en ligne est hélas fréquent et je ne me suis pas méfiée des dates... Dans les mathématiciennes, c'est Sophie Germain qui hérite souvent de la photo de la physicienne Cecilia Payne Gaposchkin.
Sonia
Enregistrer un commentaire
Une question, un commentaire ? (modération avant publication)