La preuve qu'une femme peut faire trois choses à la fois...

- Porter 15 livres sur la tête,
- Résoudre un Rubik's Cube
- Réciter les 100 premières décimales de Pi...

Ça ne sert à rien ? Certes, mais essayez donc d'en faire autant !

La semaine sainte des profs...

En voyant la foule de gens, Jésus alla sur la montagne.

Et lorsqu'il fut assis les douze apôtres vinrent à lui.

Il leva les yeux sur ses disciples et fit son sermon :

"Bienheureux les pauvres en esprit, car le royaume des cieux est à eux.
Bienheureux ceux qui souffrent, car ils seront consolés.
Bienheureux les doux, car ils posséderont la terre.
Bienheureux ceux qui ont faim et soif de justice, car ils seront rassasiés.
Bienheureux les miséricordieux, car ils obtiendront miséricorde.
Bienheureux ceux qui ont le cœur pur, car ils verront Dieu.
Bienheureux les pacificateurs, car ils seront appelés fils de Dieu.
Bienheureux ceux qui seront persécutés pour la justice, car le royaume de Dieu leur appartient"

Aussitôt, Simon Pierre dit : "Est-ce qu'on doit apprendre tout ça ?"

Et André dit : "Est-ce qu'il fallait l'écrire ?"

Philippe dit : "Je n'ai pas de feuille".

Jean dit : "Les autres disciples n'ont pas eu à l'apprendre, eux !"

Thomas continua à faire ses exercices de mathématiques.

Barthélemy dit : "C'est coefficient combien ?"

Jacques dit : "Est-ce qu'on sera interrogé sur tout ?"

Marc dit : "Ça comptera dans quel trimestre ?"

Matthieu quitta la montagne sans attendre et dit : "Je vais aux toilettes !".

Jude dit : "Vous avez dit quoi après pauvres...?"

Et Simon le zélote dit enfin : "Ça va bientôt sonner !"

Alors un grand prêtre du temple qui était présent à l'arrière s'approcha de Jésus et lui demanda :

"Quelle était ta problématique ? Quels étaient tes objectifs de savoir-faire ? Les socles de compétence ? Pourquoi ne pas avoir mis les disciples en situation ? Et en activité de groupe ? Pourquoi cette pédagogie frontale ?" …

Alors Jésus s'assit et pleura...

Merci à Isabelle, ma collègue d'histoire, pour le fou-rire de ce soir...

Combien de rectangles y a-t-il dans un quadrillage ?

On considère un rectangle quadrillé, composé de C colonnes, et de L lignes. Combien de rectangles peut-on former ? La réponse est :

(La preuve est laissée au lecteur, à titre d'exercice ;-D)

Prenons un exemple facile pour nous convaincre que cette formule est valable :

Application concrète : 

Combien de rectangles pouvez-vous obtenir avec cette tablette de chocolat (on précise que ce chocolat est noir, avec minimum 52% de caco ;-))

Le prix Abel des mathématiques décerné à John Tate

 Le prix Abel de mathématiques a été attribué aujourd'hui à l'Américain John Tate "pour l’étendue et le caractère durable de son influence sur la théorie des nombres" utilisée pour le stockage informatique des données, a annoncé l'Académie norvégiennes des Sciences et Lettres.

Agé de 85 ans, le professeur Tate qui vient de prendre sa retraite de l'université du Texas, s'est dit "comblé de joie" après avoir appris la nouvelle alors qu'il "allait prendre sa douche". Le prix de 6 millions de couronnes (un million de dollars) devrait lui être remis le 25 mai par le roi Harald de Norvège.

John Tate a été "un architecte de premier ordre" dans le développement de la théorie des nombres, un "monde (qui) s'étend des mystères des nombres premiers à la façon dont nous stockons, transmettons et protégeons l'information dans nos ordinateurs modernes", a estimé le jury. Avant de rejoindre l'université du Texas, le mathématicien a enseigné dans plusieurs universités américaines prestigieuses: Princeton, Columbia et Harvard. Elu à l'Académie nationale américaine des sciences en 1969, il a également été nommé membre à titre étranger de l'Académie française des sciences et membre honoraire de la Société mathématique de Londres.

Le prix Abel, du nom du mathématicien norvégien Niels Henrik Abel (1802-1829), a été créé par le gouvernement norvégien avec l'objectif de combler l'absence de prix Nobel de mathématiques. Trois Français l'ont remporté depuis sa première attribution, en 2003.

Source : Le Figaro.fr

Photos de symétries dans la nature, l'architecture, le quotidien

J'ai organisé un concours de photos dans ma classe de 5ème, avec pour thème les symétries centrales et axiales. Une douzaine d'élèves a participé et j'ai récolté une cinquantaine de photos.

Voici un pèle-mêle des productions des élèves et les deux photos arrivées médaille d'or ex-aequo (le jury était composé de deux directrices, et de plusieurs profs).

Cela va de la bouée de sauvetage aux feuilles d'arbre, en passant par les reflets de lacs et les tapis persans...

 Cliquez pour zoomer

Bravo à Louis :

Bravo à Domitille :

400ème post : Poème de Desnos "L'anneau de Möbius"

L'anneau de Möbius

Le chemin sur lequel je cours
Ne sera pas le même quand je ferai demi-tour
J'ai beau le suivre tout droit
Il me ramène à un autre endroit
Je tourne en rond mais le ciel change
Hier j'étais un enfant
Je suis un homme maintenant
Le monde est une drôle de chose
Et la rose parmi les roses
Ne ressemble pas à une autre rose.

(Lire l'article d'AlgoRythmes expliquant l'anneau de Möbius)

Jolies courbes : saison des fleurs

Gallica s'enrichit et s'embellit

Gallica n'est ni une femme légère, ni une ville, mais bien cette bibliothèque nationale en ligne que je vous avais présentée il y a quelques temps. Les collections numérisées sont de plus en plus complètes, et le site a fait peau neuve. N'hésitez pas à y refaire un tour !

Gallica a franchi le cap du million de documents mis à la disposition des internautes. Cette étape importante témoigne de l’enrichissement continu et soutenu de la bibliothèque numérique et de l’accélération donnée aux programmes de numérisation.

La répartition par type de document s’établit de la manière suivante :
S’agissant des documents de la BnF :
- plus de 153 000 ouvrages, dont 97 000 disponibles en mode texte
- plus 688 000 fascicules de périodiques, dont 298 000 en mode texte
- plus de 118 000 images
- plus de  9 700 cartes et plans
- plus de 1 000 documents sonores
- plus de 4 500 manuscrits
- plus de 2 400 partitions

- plus de 8 000 documents des bibliothèques partenaires

- plus de 22 000 documents de l’édition contemporaine

Et Gallica s'inscrit dans la modernité : pour accompagner le lancement de la nouvelle interface de son site et promouvoir les contenus et les services de la Bibliothèque numérique, une page Facebook a été créée, ainsi qu’une page Netvibes.

Chocolate Factory nous régale

The most honest chocolate tablet
Manger du chocolat est un réel plaisir parfois difficile à contrôler. Se laisser tenter par un carré de chocolat, puis un autre, jusqu’à manger la moitié de la tablette fait souvent culpabiliser. D'un autre côté, rester sur sa faim est bien dommage et peut aussi provoquer une frustration. Alors comment gérer sa consommation pour respecter son apport calorique ? "The most honest chocolate tablet" nous met face à nos responsabilités en nous annonçant clairement les calories de chaque morceau. Plus besoin de chercher au dos de la boîte, ni de faire le dur calcul de l’apport calorifique de notre dégustation.
Cette tablette dessinée sur l’archétype d’un histogramme, nous propose différents carrés hiérarchisés en fonction du plaisir que nous décidons de nous accorder :
34 Kcal, 68 Kcal, 102 Kcal, 136 Kcal, 170 Kcal, 204 Kcal, 238 Kcal ou encore 272 Kcal !
Le lecteur ne manquera pas d'observer que la progression de ces valeurs est arithmétique (+34). Je suppose que dans l'emballage, deux plaquettes du modèle ci-dessous sont rangés tête-bêche.

Ce même fabriquant propose également de délicieux diagrammes circulaires en turrón (nougat hibérique) recouvert de chocolat.

Et chez un concurrent, on trouve cette tablette permettant de compter les calories :

Nombres belges et Kangourou de midi

Un nombre belge est un nombre qu'il est possible d'atteindre en additionnant successivement son chiffre des dizaines puis son chiffres des unités, puis des dizaines, puis des unités et ainsi de suite, jusqu'à obtenir le nombre en question.

Exemple : 26 est belge, car 2 + 6 + 2 + 6 + 2 + 6 + 2 = 26

Contre-exemple : 15 n'est pas belge, car 1 + 5 + 1 + 5 + 1 est inférieur à 15, et 1 + 5 + 1 + 5 + 1 + 5 est supérieur à 15.

Saurez-vous me dire quels nombres sont belges entre 41 et 49 ?

Cette question est extraite du "Kangourou de midi 2010". Il s'agit de la version hors-compétition du concours Kangourou qui a eu lieu ce jeudi 18 mars, et auquel ont participé nos élèves de 5ème. Le Kangourou de midi est destiné à mettre une bonne ambiance dans la cantine des profs le jour du concours, en proposant des devinettes amusantes et en rapport avec plusieurs disciplines scolaires.

Voici le sujet complet (cliquer pour zoomer) :

La revue Accromath

Accromαth est une revue canadienne semi-annuelle produite par l'Institut des sciences mathématiques et le Centre de recherches mathématiques. S'adressant surtout aux étudiants et enseignants d'école secondaire et de cégep, la revue est distribuée gratuitement dans les écoles secondaires et les cégeps du Québec. (Peut-être Missmath peut-elle confirmer que ce magazine est de qualité ?)

Les thèmes abordés sont très variés, et très souvent en lien avec "la vraie vie", par les maths appliquées à la biologie, à l'économie, à l'astronomie, à la musique et j'en passe !

On trouve également des défis mathématiques, des dossiers sur des mathématiciens.

Ça me semble être une mine d'infos rigoureuses et intéressantes autour des maths, un peu dans l'esprit de la revue française Tangente.

Les archives sont consultables en PDF sur le site de la revue.

Le prix du millénaire pour Grigori Perelman

La résolution de la conjecture de Poincaré, l’un des problèmes mathématiques les plus difficiles posés au 20ème siècle, vaut au Russe Grigori Perelman l’attribution d’un Prix du Millénaire par l’Institut Clay pour les mathématiques.

Lisez l'article du NouvelObs (avec Sciences et Avenir)
ou celui du JDD.

Florilèges d'appréciations de bulletins politiquement correctes

Le second trimestre touche à sa fin. Voici donc quelques appréciations (qui circulent sur internet).

Désormais, sur le bulletin des élèves,

on ne doit plus écrire… mais il convient de noter...

"Il est fainéant" mais "Il manifeste un léger déficit de motivation induisant une phase de repos intellectuel qui n’est probablement que temporaire…"

"Il est très paresseux" mais "Il ne présente aucune appétence génétique manifeste pour le travail scolaire et se montre réfractaire à toute dépense d’énergie intempestive…"

"Il a un poil dans la main" mais "Ses caractéristiques génétiques l’empêchent de tirer le meilleur parti de tout le potentiel de ses membres supérieurs…"

"Il ne fait rien" mais "On ne trouve nulle trace concrète ni même virtuelle de son activité débordante, mais sa volonté de bien faire commence à devenir perceptible…"

"Il est nul" mais "Les objectifs pédagogiques sont inadaptés à ses potentialités, mais sa marge de progression n’en de-meure pas moins substantielle…"

"Il est bête" mais "Ses connexions cérébrales ne sont pas encore toutes assurées, mais le processus de réflexion devrait connaître un déblocage imminent…"

"C’est un abruti" mais "Il connaît un épanouissement ralenti, mais certaines lueurs indiquent qu’il ne demande qu’à s’éveiller à la moindre étincelle…"

"Il ne sait rien" mais "L’imprégnation cognitive résiduelle n’est pas encore quantifiable, mais on constate des progrès méthodologiques dans l’ouverture du cartable…"

"Il ne retient rien" mais "Ses capacités mnémotechniques sont encore peu développées en raison d’une carence en phosphore…"

"Il a des difficultés" mais "Il pourrait certainement mieux faire si le contexte s’y prêtait et que les lacunes rédhibitoires ne cessaient de croître de façon exponentielle…"

"Il dort en classe" mais "Il connaît un léger décalage horaire et son horloge biologique semble réglée sur l’heure estivale de l’hémisphère sud…"

"Il fait des bêtises" mais "Son manque de maturité implique des comportements déviants peu propices à maintenir son attention et son sérieux…"

"Il fait le clown" mais "Son sens inné de la plaisanterie le conduit à distraire ses camarades et à animer le cours sans se soucier de l’ordre établi…"

"Il monte sur les tables" mais "Il recherche le meilleur point de vue panoramique et tente d’oxygéner davantage les cellules de son cerveau afin d’augmenter sa productivité…"

"Il court dans la classe" mais "Sa motivation irrépressible à rendre service enrhume un peu ses voisins, mais sa vitesse de course fait merveille en gymnastique…"

"Il est violent" mais "Son instinct possessif et revendicatif le pousse à des actes impulsifs qu’il regrette immédiatement, malgré ses récidives chroniques…"

L'hypermnésie de Daniel Tammet

Apparemment, le sujet "Daniel Tammet" a attiré beaucoup de monde sur ce blog depuis deux jours.

Si vous avez raté l'émission d'hier soir, vous pouvez la revoir en cliquant ici pour accéder au site de l'émission Prise Directe. La partie du sujet qui évoque Tammet démarre aux environs de 1h30 (placez le curseur à ce moment-là si c'est lui qui vous attire).

Daniel Tammet dans Prise directe sur France 2 ce soir à 20h35

Plateau-télé ce soir :-)

Je vous ai parlé hier de Daniel Tammet, il intervient dans l'émission informative/culturelle Prise directe, présentée par Béatrice Schönberg. Le thème en sera :  

Amnésie, Faux-souvenirs, Manipulations :

les mystères de la mémoire

• Perdre la mémoire à 40 ans

Fabienne, 44 ans, est atteinte de la maladie d'Alzheimer depuis 7 ans. Elle gagne du temps sur l'oubli en voyageant avec son mari avant le grand trou noir. André, 40 ans, souffre d'amnésie sévère suite à une attaque.

• Ils manipulent nos souvenirs

Comme Sophie, Bernard et sa femme sont tombés sous la coupe d'un thérapeute qui les a convaincus de mauvais traitements dans leur enfance. Jean, un spécialiste de l'hypnose, aide quant à lui ses patients à rendre acceptable le souvenir d'un traumatisme.

• Mémoire hors norme

Les hypermnésiques, ce sont des surdoués de la mémoire. Ils développent des capacités prodigieuses en calcul, aux échecs, en musique. Mais dans certains cas, cette hypermnésie peut devenir un handicap car la mémoire ne trie plus les souvenirs. (Témoignage de Daniel Tammet)

Daniel Tammet : "Je suis né un jour bleu"

Cela fait longtemps que je ne vous ai rien recommandé pour votre bibliothèque. Comme hier, c'était la journée de Pi, je saisis l'occasion pour vous présenter Je suis né un jour bleu écrit par Daniel Tammet.

Il s'agit d'un témoignage autobiographique d'un homme atteint d'une forme d'autisme appelée syndrome d'Asperger, une forme légère d'autisme qui s'accompagne chez lui :

• de quelques difficultés d'interaction sociale. 
• d'une mémoire hors du commun. Par exemple Daniel maîtrise (actuellement) 11 langues  et pense pouvoir apprendre en une semaine n'importe quelle langue. Par ailleurs, il a appris en 3 mois les 22 514 premières décimales de Pi, et les a récitées en 5 heures, 9 minutes et 24 secondes, le 14/03/04, (journée de Pi). Ce défi était destiné à récolter des fonds pour la recherche sur l'épilepsie, je crois.
• de synesthésie, c'est-à-dire un phénomène neurologique associant plusieurs sens. Par exemple pour Daniel, le mercredi est associé à la couleur bleue, et chacun des nombres est associé à une couleur, une texture ou une position dans l'espace (ce qui lui permit d'établir le record sur Pi).

Ce livre est très touchant, et le point de vue de Daniel Tammet sur les nombres et les mathématiques est enrichissant.

Découvrez le documentaire The boy with the incredible brain sur Google Vidéo (en anglais), vous y verrez une partie de la récitation des décimales de Pi par l'auteur.

Ou bien cette vidéo en français, extraite de l'émission On n'est pas couché

Allez lire le poème-hommage à Pi écrit par Daniel Tammet à l'occasion de la journée de Pi 2009.

Apple Pi...

A l'occasion de la journée de Pi, voici plusieurs images à jeu de mots sur l'apple pie dont vous trouverez la recette ici.

Trouver une séquence de chiffres dans les décimales de Pi

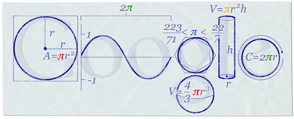
Logo Google du jour :

L'an dernier je vous présentais la fête de Pi. Aujourd'hui, je vous donne un lien vers un site permettant de trouver une séquence de chiffres dans les décimales de Pi (votre date de naissance ou tout autre nombres extrêmement important ;-).

J'ai fait le test pour 14032010 (soit la date d'aujourd'hui au format français), voilà où cette séquence a été trouvée :

Message publié le 14/03 à 03h14

Promenade géométrique et printanière à Villandry

Voici la suite de notre promenade aux jardins de Villandry commencée il y a deux jours. Cliquez pour zoomer.

Promenade hivernale et géométrique aux jardins de Villandry

Le château de Villandry est un château de la Loire d'architecture Renaissance situé à 15 km à l'ouest de Tours. Il est connu pour ses trois jardins à la Française, son donjon qui domine un potager décoratif (1 ha), son jardin d'ornement et son jardin d'eau. Il a obtenu le label "Jardin remarquable" créé en 2004 par le Ministère de la culture.

Je me demande quels instruments sont utilisés pour créer les tracés géométriques des massifs à la française...

Voici quelques photos de ce jardin téléchargées sur le site officiel du Château, avec aujourd'hui une sélection hivernale.

(cliquez pour zoomer)

Rendez-vous dans deux jours pour la promenade printanière !

Les mathématiques à l'assaut du crime

Trouverez-vous cet article vraiment convaincant... (et clair) ?

L’équipe de Martin B. Short, du Département de mathématiques de l’Université de la Californie, présente « un système d’équations qui permettrait de déterminer d’avance les endroits où des crimes sont susceptibles de se produire ». Ce système se base sur des évidences tirées de l’analyse des mouvements, des actions et des intentions des criminels. Pour anticiper les crimes dans le temps et l’espace, l’équipe de recherche a utilisé un système mathématique de réaction-diffusion. On peut utiliser cette formule pour plusieurs types de crimes afin de les analyser de façon indépendante, précise t-on. 

Un lieu x dans un environnement y
L’équation mathématique est en elle-même complexe. Les chercheurs identifient dans un premier temps une valeur x, représentant la zone où l’on souhaite analyser le niveau de criminalité. Chaque zone x est caractérisée par les variables x ; y : les cibles et le temps. En somme, le risque de criminalité se calcule en additionnant les variables dynamiques et stables.

Le champ de risque A(x,t) est pour sa part décrit par une variable stable A et une variable dynamique B. La variable A est statique dans le temps mais dynamique dans l’espace, et ne se couple qu’avec le facteur qui représente les cibles. Le facteur B, dynamique dans le temps mais stable dans l’espace, se couple pour sa part au facteur qui représente le temps dans l’équation de base du champ de risque.

Dans un deuxième temps, l’équation considère la densité potentielle des agents criminels. La variable k calcule finalement le potentiel de croissance du crime dans une zone x.

L’utilité de l’équation pour les forces policières repose de ce fait sur le facteur de croissance du crime qui révèle les forces d’attraction qui motivent les criminels à revenir dans les zones ou des crimes ont été commis avec succès.

L’étude souligne par ailleurs que bien que le crime soit un fléau qui touche toutes les villes modernes, tous les quartiers n’en sont pas affectés au même niveau. Les analyses de mouvement de l’étude permettent donc d’identifier plus précisément ces zones, et les équations formulent une hypothèse quant aux autres endroits avoisinants où les activités criminelles pourraient se déplacer. M. Short fait valoir que les conséquences de l’incompréhension des méthodes de détection des zones à risque  retombait jusqu’à présent sur les épaules des agences policières.

Encore aujourd’hui, on peine à cibler les endroits où il faut mobiliser du personnel en Californie. Si les policiers ne sont pas assez répressifs dans les zones  à risque, la criminalité augmente en raison de la mauvaise répartition du personnel policier, mentionne Short. « Si un plus grand nombre de policiers était dépêché dans les zones à risques découvertes par nos méthodes mathématiques, il serait possible de faire diminuer le crime »,  conclut M. Short, justifiant l’utilité de son équation.

Source : Impact Campus (Canada)